Nakamura Inasa Professor

Research overview

Surface-knots in the four-dimensional space. My research interest is in their construction and invariants. Focus on surface-knots among the fields of topology
My research interest is in the knot theory among the fields of topology. In particular, I focus on surface-knots and surface braids in the four-dimensional space.
A surface-knot is an embedding of a closed surface into the four-dimensional space and is a field of classifying an equivalent class under ambient isotopy by using a variety of invariants. The “invariants” herein refer to mathematical quantities that give the same value for equivalent surface-knots.

■ Surface-knots in the four-dimensional space
The theory of one-dimensional knots in the three-dimensional space dates back to Gauss’ paper published in 1833 and covers a range of targets including application to the structure of DNA and protein. Target of my research, surface-knots in the fourth dimension, goes back to 1925, in which year Artin constructed spun two-dimensional knots from one-dimensional knots.
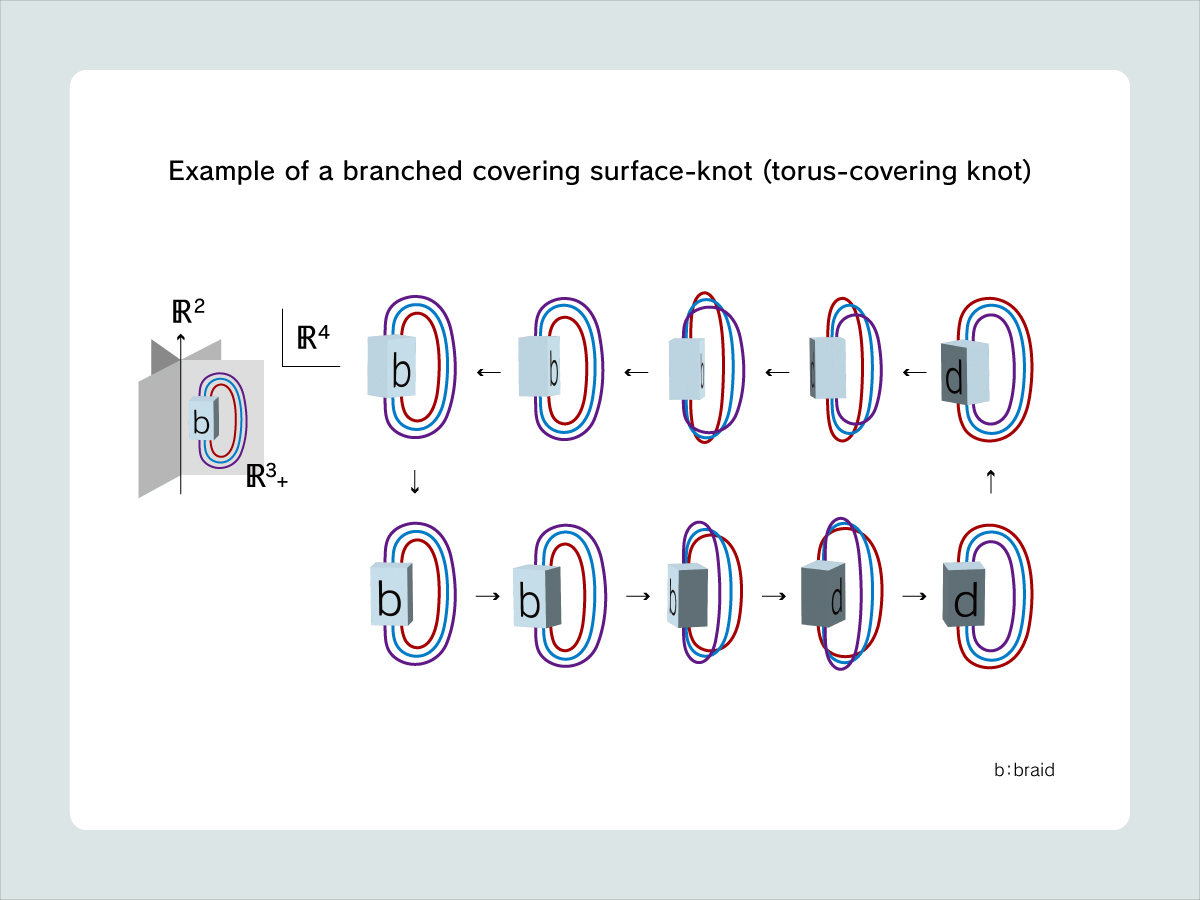
In particular, among the surface-knots, I focus on the branched covering surface-knot, a surface-knot in the form of a branched covering over a surface-knot. It includes a torus-covering knot. The “torus-covering knot” is defined as a surface knot in the form of a branched covering over the trivial standard embedded torus. While two-dimensional knots, embeddings of a sphere, have been studied in various ways, research on surface-knots with positive genus has not yet been widely developed. Through research on, for example, torus-covering knots, I intend to disclose the properties of surface-knots that are not found among two-dimensional knots.
Time transformation of a graph can be represented in the shape of a knotted surface. I will study how to handle this surface by using the theory of surface-knots.

■ New applications in fields such as life science are hopeful
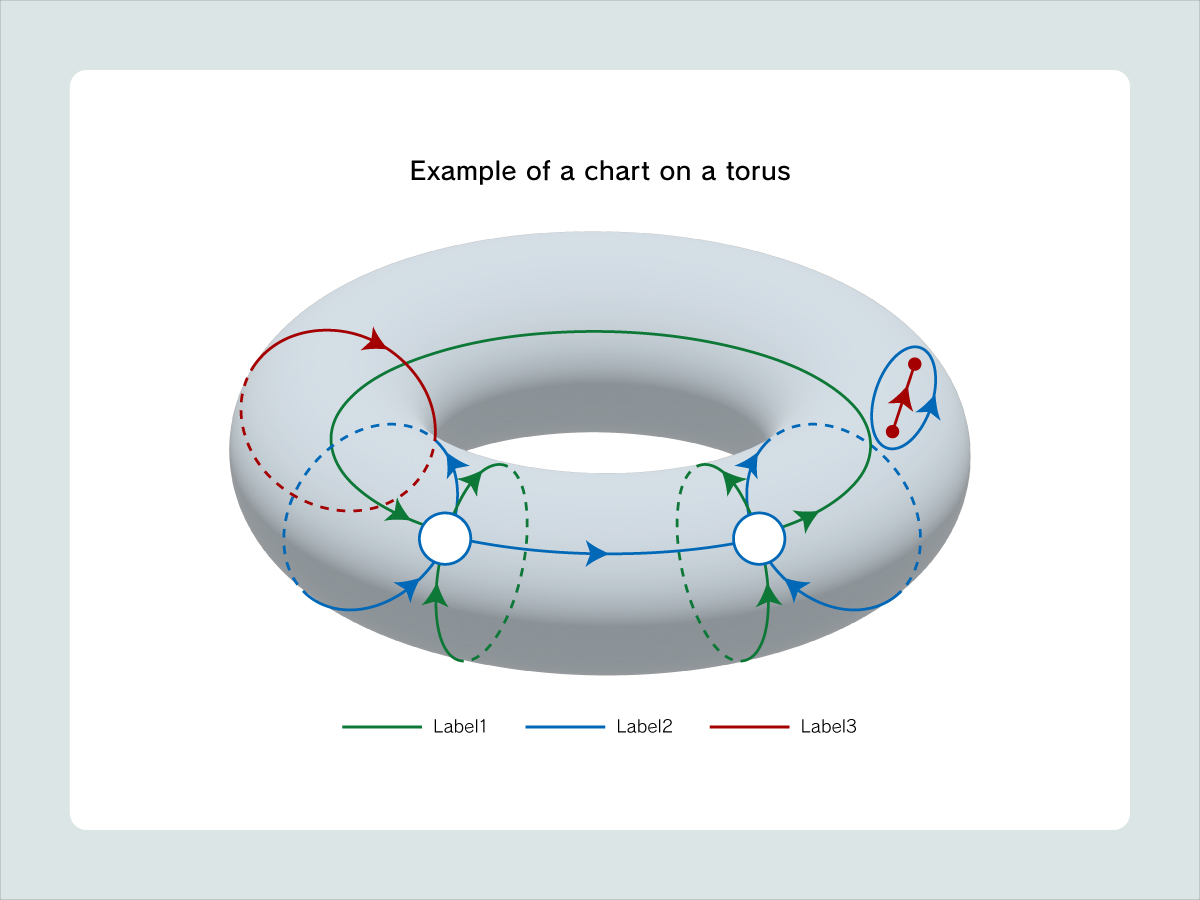
Research on the knot theory is not limited to handling of formulas; in fact, it involves the process of writing on paper or forming a knot with a string, in other words, it uses a visible target—this process interests me. My study method uses, in principle, hand calculation and handwriting. Because the branched covering surface-knots are in the form of a curved covering, I focus on the transformation by using the chart description representing changes in the fourth dimension that is otherwise invisible and examining the calculation method and properties of invariants. Other attempts include research on a knotted surface as the closure of surface braids and a knotted surface representing the process of graph transformation process.
While it is not easy to derive invariants of surface-knots, I feel happy and challenged when I have succeeded in solving or demonstrating my several months old problem.

Although what fields or research projects will have a relation with research on knots is unknown, I expect that knots will be further applied to and studied in life science and other fields.