中村 伊南沙 教授

研究概要

4次元空間内の曲面結び目。 その構成や不変量を研究しています。 トポロジーの中でも曲面結び目に着目
私はトポロジー（位相幾何学）の分野でも、結び目理論について研究しています。特に、4次元空間内での「曲面結び目」と「曲面ブレイド」に注目して取り組んでいます。
「曲面結び目」とは４次元空間の中への閉曲面の埋め込みであり、全同位による同値類をさまざまな不変量を用いて分類する分野です。ここで、「不変量」とは、同値な結び目については同じ値を与える数学的量のことです。

4次元空間内の曲面結び目について
３次元空間内の１次元の結び目理論は 1833年のGaussの論文にまで遡ることができ、DNAやタンパク質の構造などへの応用も含め広く研究対象とされてきていますが、私が対象としている4次元内の「曲面結び目」は、1925年Artinが１次元の結び目からスパン２次元結び目を構成したのが始まりです。
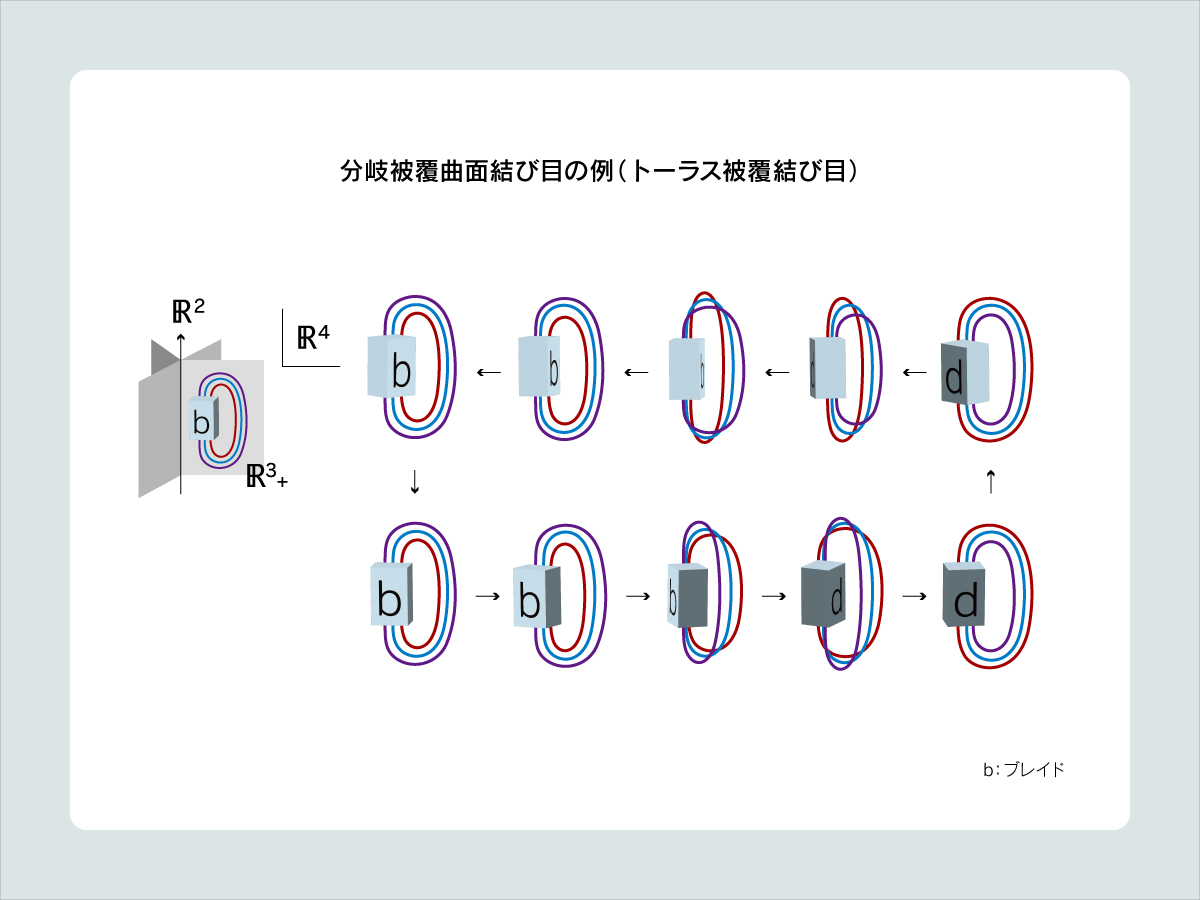
私は曲面結び目の中でも特に、曲面の被覆の形をした「分岐被覆曲面結び目」について研究していますが、そこには「トーラス被覆結び目」を含みます。「トーラス被覆結び目」は、標準的に埋め込まれた自明なトーラス上の分岐被覆の形で表せる曲面結び目として定義されます。これまで球面の埋め込みである「２次元結び目」についてはいろいろな研究がなされてきましたが、一般の種数の曲面結び目についての研究はそれほど発展していません。「トーラス被覆結び目」などを研究することで、２次元結び目では見られない曲面結び目の性質を明らかにしていきたいと思います。
また、グラフの時間変形は曲面の形で表せますが、この曲面の扱い方を曲面結び目の理論を用いて考察したいと考えています。

生命科学などの分野で新たな応用を期待
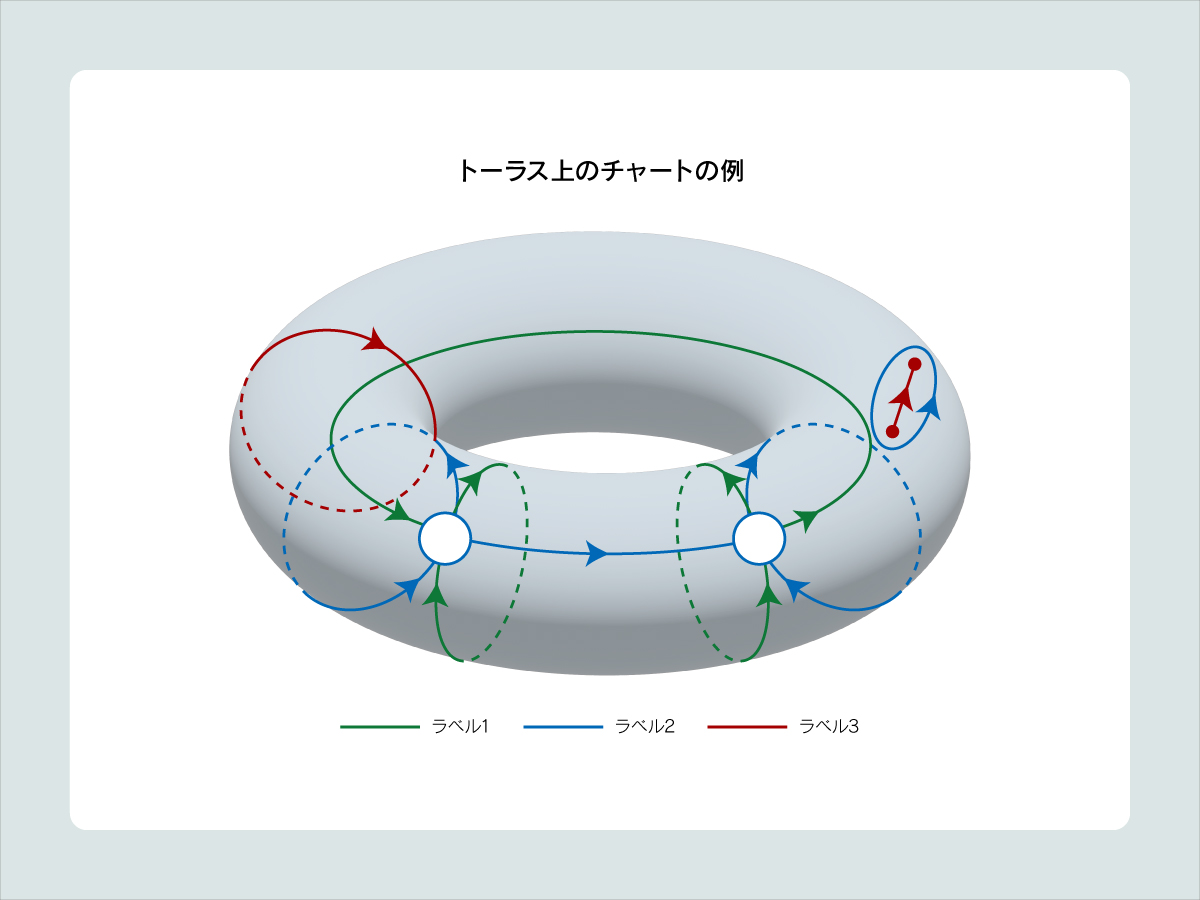
結び目理論の研究は式だけを扱うのではなく、実際に紙に書いたり紐で作ったりと、対象が見えるのがおもしろいところです。私の研究方法も基本的には手計算や手書きであり、曲面の被覆の形をした「分岐被覆曲面結び目」については、本来なら見えない4次元内の変化を表現した「チャート表示」を用いてその変形について研究し、不変量の計算方法や性質を調べています。またそれ以外にも、「曲面ブレイド」の拡張となるような曲面や、グラフの変形過程を表す曲面などについて研究しています。
こうして積み重ねた研究で「曲面結び目」の不変量を導き出すのは簡単ではありませんが、何か月も考えていたことがぱっと解けた時や証明できた時はうれしいし、やりがいを感じます。

結び目の研究自体が、これからどんな分野・どんな研究と結びついていくのか未知数ですが、たとえば生命科学などの分野でも結び目の応用や研究が進んでいくことを期待しています。